Existe una constante que desde los tiempos de la antigua Grecia y a lo largo de la historia ha despertado interés en matemáticos, científicos, filósofos, artistas y arquitectos: La proporción áurea, ¿el secreto de la belleza perfecta?. Esta curiosa y elegante relación matemática que está presente en diversos patrones y formas en la naturaleza ha tenido una influencia significativa en arquitectura y diseño por ser considerada una proporción que permite crear composiciones naturales, orgánicas y visualmente muy agradables.
¿Qué es la proporción áurea?
La proporción aurea también conocida como sección o razón aurea, número de oro o divina proporción, ha sido utilizada durante siglos por quienes buscan la belleza, la armonía y el equilibrio, y ha obsesionado a muchos matemáticos, artistas, arquitectos y diseñadores a lo largo de la historia.
Se dice, que por primera vez fue reconocida por algún matemático griego que observó la proporción existente entre la altura inclinada y la mitad de la longitud de la base de las pirámides de Egipto, a la que le atribuyó la causa de la increíble belleza y perfecta armonía de que gozan.
Pero no fue hasta el año1509 con la publicación del libro (De divina proportione) Sobre la proporción divina,de la matemática italiana Luca Pacioli que se presentara esta proporción como símbolo de la simplicidad y el orden, que se hiciera famosa entre artistas y matemáticos, y que muchos fascinados por ella, dijeran que es agradable a la vista por naturaleza por estar presente repetidamente en esta y que es la representación matemática de la belleza.
Lo más asombroso de esta proporción es la forma en que aparece repetidamente en diversos patrones y formas en la naturaleza. La vemos por todas partes: en la disposición de los pétalos en flores, en la espiral de algunas conchas marinas, en la disposición de las ramas y hojas en árboles y a menudo en la relación entre el grosor del tronco y el de sus ramas, en las espirales de una piña, en los colmillos de un elefante, en la estructura de los huracanes entre otros muchos casos. Y también en el cuerpo humano, es curioso que en cada individuo, la relación entre su altura total y la distancia entre su ombligo y la planta de sus pies es el número áureo, así como entre diferentes distancias en el rostro. La proporción áurea describe una relación especial entre las partes de un elemento o entre varios. Esta parece ser la mejor proporción entre dos partes desiguales, y quizá el sistema de proporciones más conocido.
Aunque numéricamente no es más que la relación entre dos partes diferentes, una proporción geométrica expresada por un número irracional aproximadamente igual a …1.618033988 que está representado por la letra griega (fi) phi (φ).
Relación entre la proporción aurea y la sucesión de Fibonacci
Existe una estrecha relación entre la proporción aurea y la sucesión de Fibonacci, esta última es una serie numérica infinita que empieza por: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55… en la que la suma de dos de sus números consecutivos es el siguiente número, el segundo más el tercero da como resultado el cuarto, el tercero más el cuarto nos da el quinto y así sucesivamente. Cuando dividimos cada uno de los números entre su anterior el resultado en la media que avanza la serie se aproxima cada vez más al número áureo 1.618
En relación aurea podemos encontrar puntos, segmentos de una recta, rectángulos, paletas de colores, así como otras construcciones geométricas.
¿Qué es el punto áureo?.
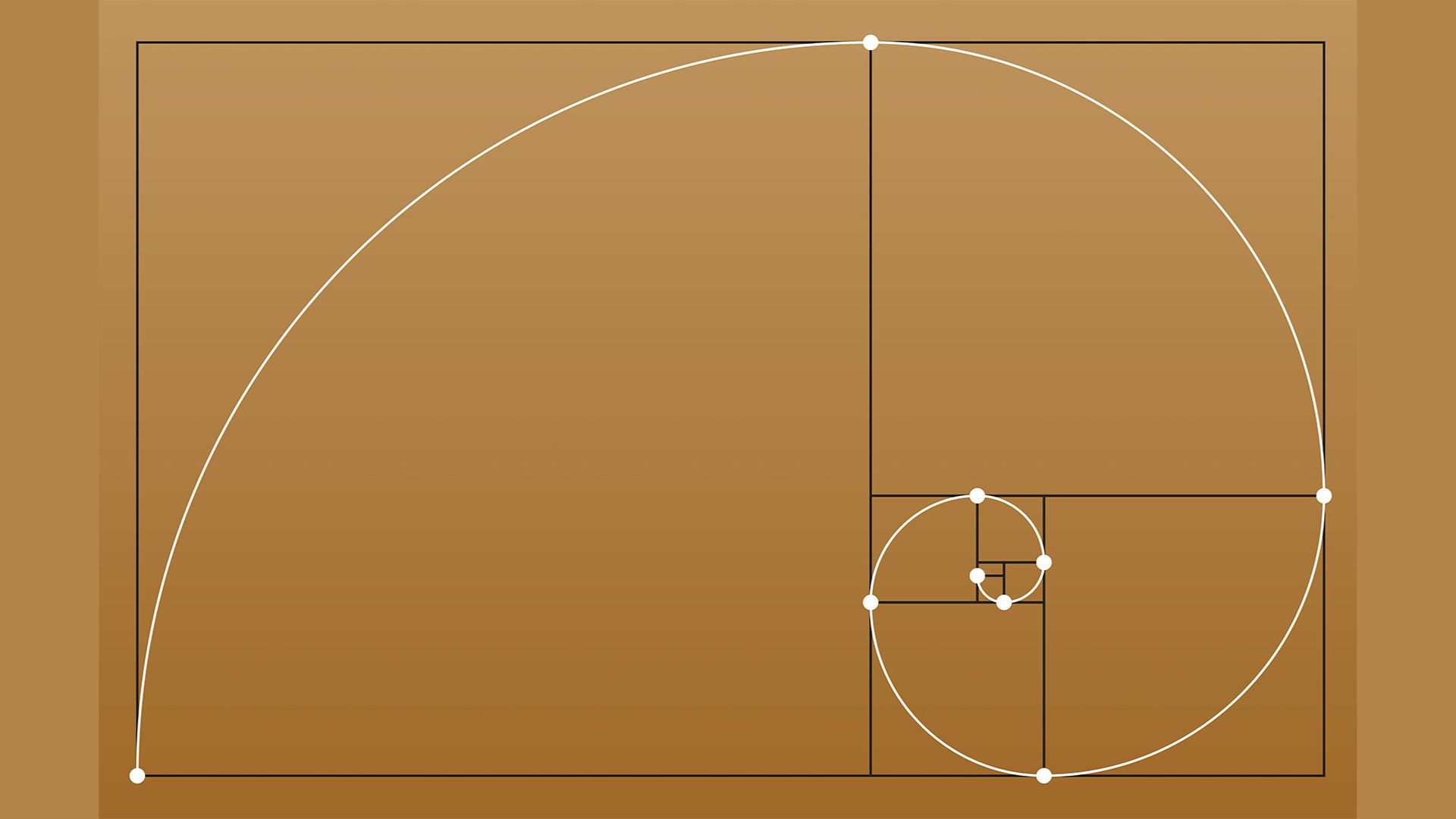
El punto áureo es el punto de donde parte una espiral áurea. Este punto es útil para marcar dónde centrar la atención en pintura, fotografía o diseño.
¿Qué es el segmento o línea aurea?.
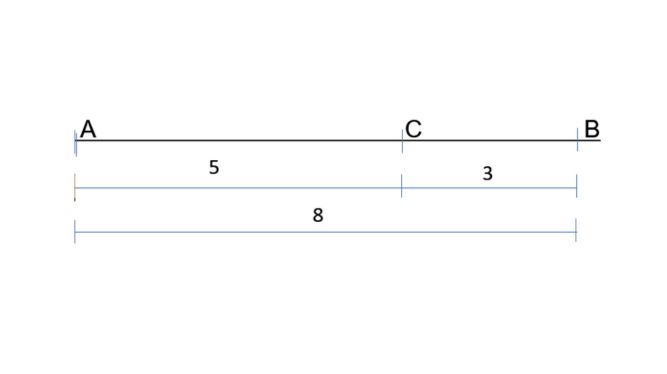
El segmento o línea aurea es el resultado de dividir una línea AB en dos partes desiguales, una mayor AC y otra menor CB de manera que la proporción entre la parte mayor y la menor sea idéntica a la existente entre la línea completa y la parte mayor.
Lo que quiere decir que:
AB/CB = 1,618 como AB/AC = 1,618
Por ejemplo: si AB es igual a 8, AC tendría que ser aproximadamente igual a 5 y CB a 3 para que estén en proporción aurea.
Entonces para construir una línea dividida en dos partes que guarden proporción aurea entre si, lo que tenemos que hacer, simplemente es, si tenemos el segmento mayor y queremos hallar el menor lo dividiremos entre 1,618 y si el que tenemos es el menor y queremos hallar el mayor lo multiplicaremos por 1,618
Pero también podremos crearlo mediante la geometría:
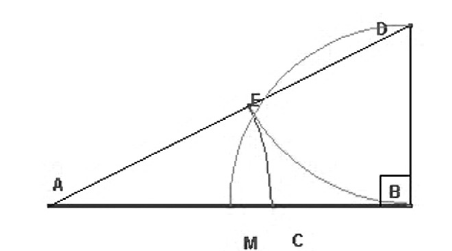
Si tenemos un segmento cualquiera AB, lo primero que tendremos que hacer es hallarle el punto medio, al que llamaremos P. Partiendo del punto B trazaremos una línea perpendicular a AB la que cortaremos con un arco de centro en B y radio BP. Al punto que se ha creado en esa perpendicular le llamaremos D y lo uniremos mediante una línea al punto A. Con centro en D trazaremos un arco de radio BD que corte la línea AD y ese será nuestro punto F, y por último con centro en A trazaremos un arco con radio AF que corte el segmento AB y será este el punto por el que quedará dividida nuestra línea armónicamente en proporción aurea.
En el diseño de interiores, esta división es muy útil para seccionar paredes a la hora de organizar la colocación de cuadros en ellas o de cualquier otro elemento, ya sea que vayamos a colgarlo también o que la pared vaya a servirle de fondo.
¿Qué es el rectángulo áureo?.
El rectángulo áureo es aquel cuya relación entre el lado más largo y el más corto es igual a la proporción áurea, aproximadamente 1,618.
Lo que quiere decir que, si tenemos un rectángulo de vértices ABCD, en el que AB es el lado largo y BC el lado corto deberá cumplirse que AB/BC = 1,618 para que guarden proporción aurea entre sí.
El rectángulo áureo tiene la particularidad de que a partir de uno se podrán obtener otros rectángulos áureos generándose así una sucesión indefinida de ellos. Esto se consigue dividiendo un rectángulo áureo en un cuadrado y otro rectángulo áureo más pequeño que será semejante al original. Con la sucesión indefinida de rectángulos áureos podremos construir una espiral áurea. Basándonos en la secuencia de Fibonacci también obtendremos un rectángulo.
¿Cómo construir un rectángulo áureo?
Al igual que en el caso de la línea aurea, para crear el rectángulo áureo podrás hacerlo bien si conoces uno de sus lados y quieres calcularlo mediante sencillas ecuaciones matemáticas o a partir de un cuadrado cualquiera mediante la geometría.
Si conoces uno de sus lados, por ejemplo, el mayor, lo que deberás hacer es dividir su longitud entre 1,618 y obtendrás la longitud del menor, y si el que tienes es el menor lo que harás será multiplicarlo por 1,618 y obtendrás el mayor.

Por ejemplo, si conoces que el lado mayor AB=6 lo que harás será dividir 6 entre 1,618 lo que es igual a 3,70. Con lo que nos queda que el lado mayor es de 6 y el menor de 3,70 pudiéndolo redondear a 4 si lo prefieres y así de sencillo habrás construido un rectángulo áureo. O utilizando la secuencia de Fibonacci si el lado más largo es 5 el más corto será 3
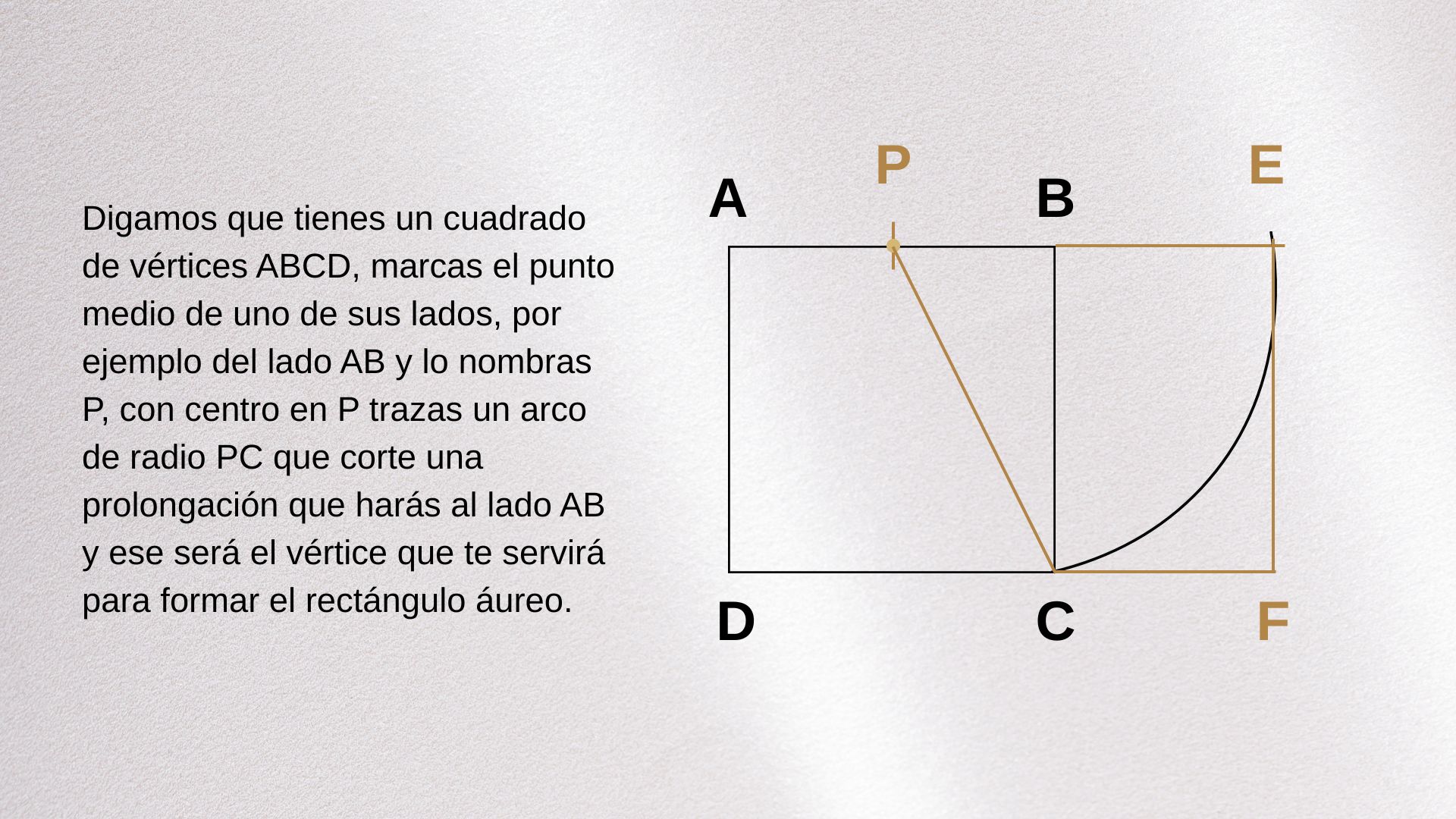
Otra forma también muy sencilla de crear el rectángulo áureo es a partir de un cuadrado cualquiera. Digamos que tienes un cuadrado de vértices ABCD, marcas el punto medio de uno de sus lados, por ejemplo del lado AB y lo nombras P, con centro en P trazas un arco de radio PC que corte una prolongación que harás al lado AB y ese será el vértice que te servirá para formar el rectángulo áureo.
Si quieres crear otros rectángulos áureos a partir de este, lo que harás será ir dividiendo la parte más estrecha del rectángulo en un cuadrado y otro rectángulo áureo más pequeño, sucesivamente.
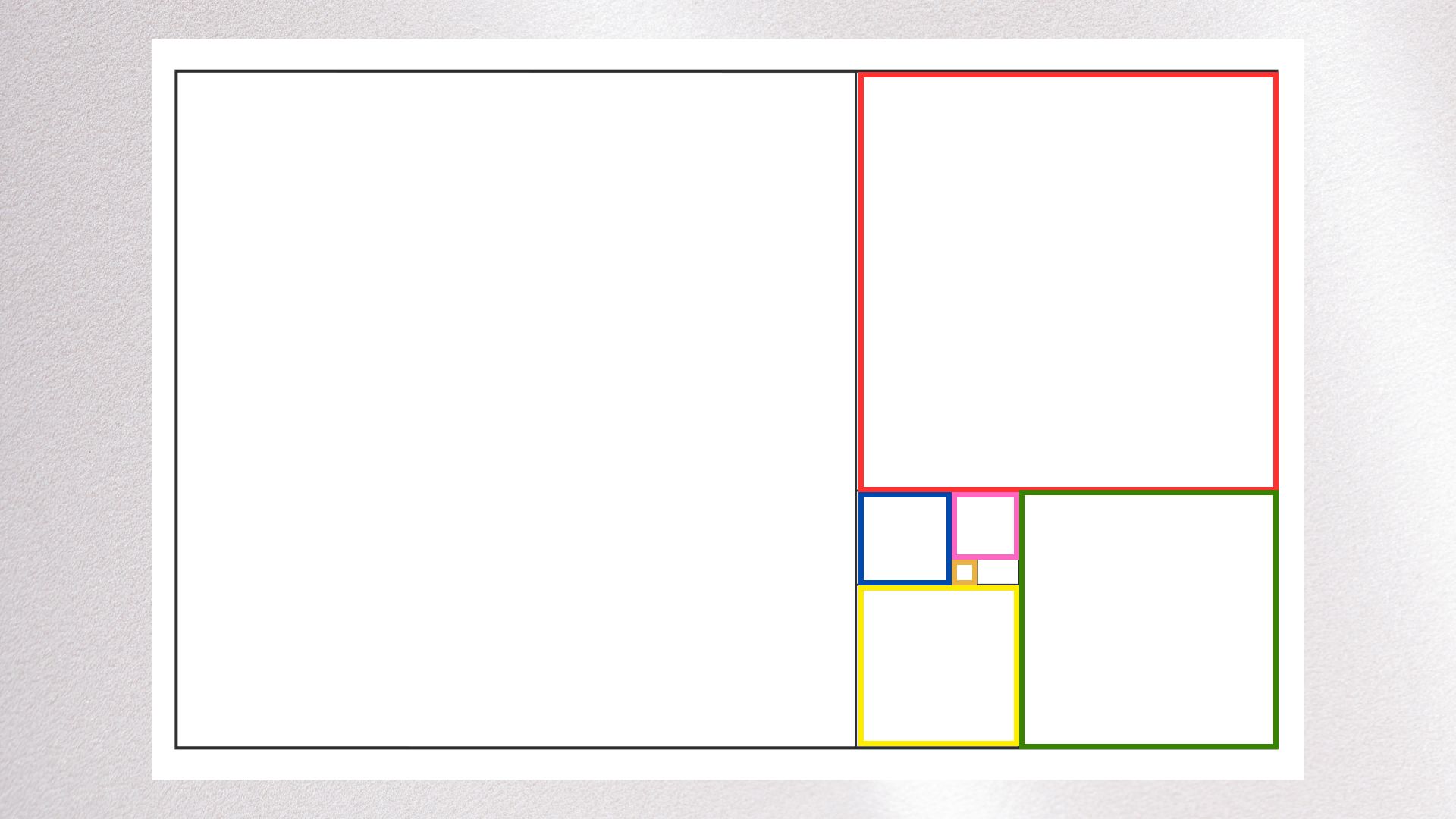
Para entenderlo mejor te mostraré un ejemplo basado en la secuencia de Fibonacci:
Construimos un rectángulo áureo en el que sus lados van a ser dos números consecutivos de la secuencia de Fibonacci.
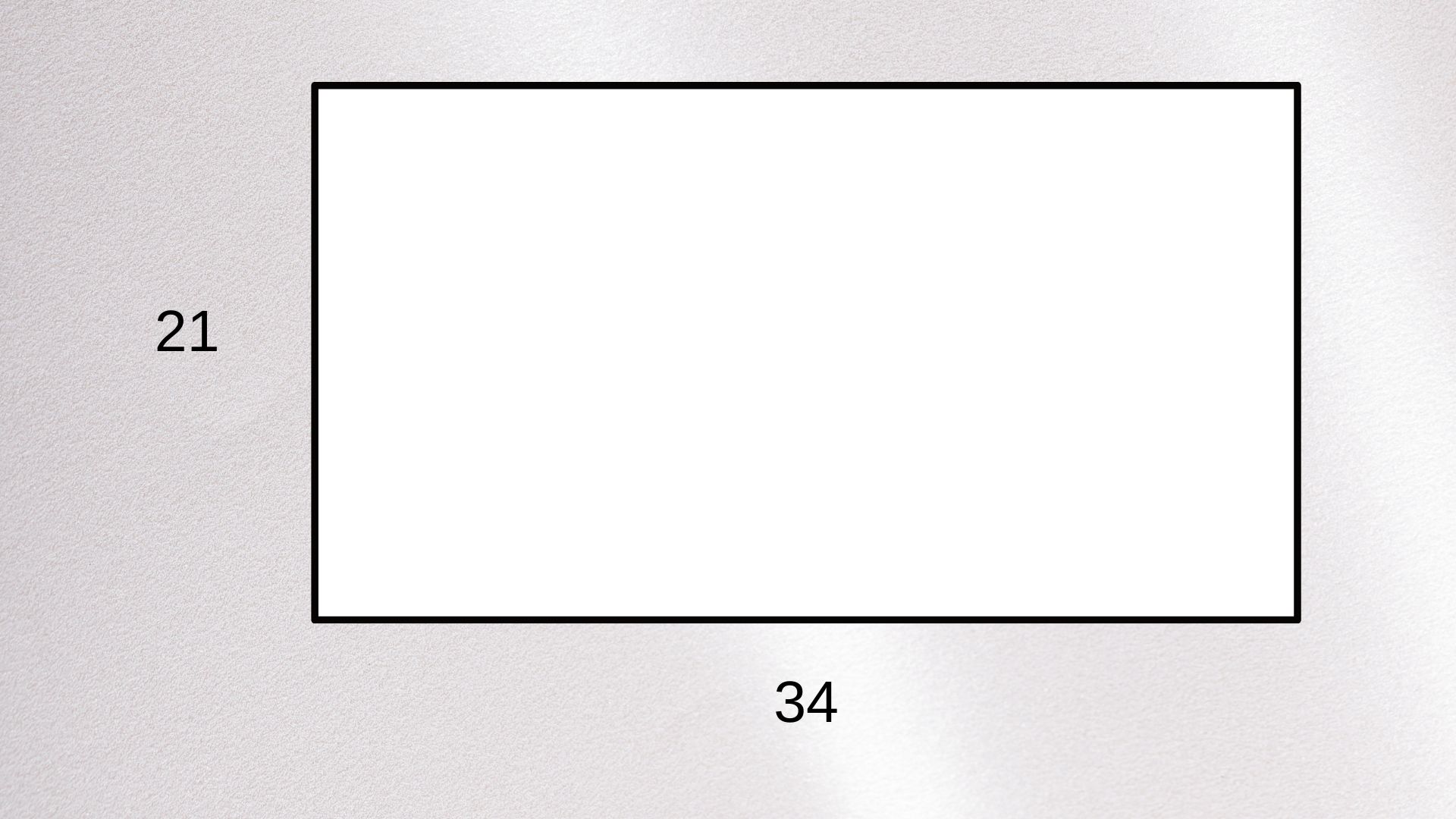
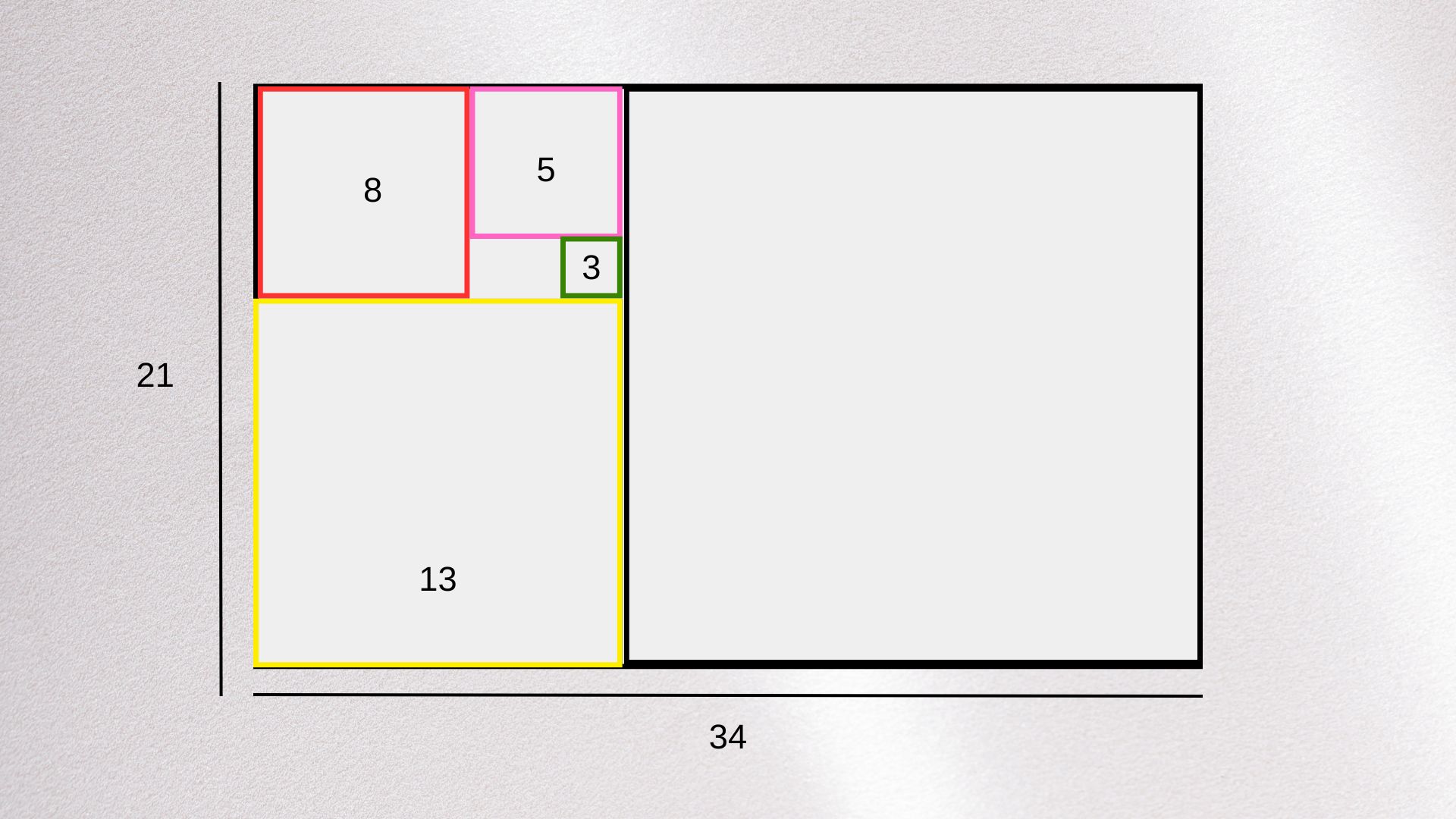
En uno de los extremos del rectángulo áureo vamos a crear un cuadrado de lado igual al número que sigue al número que corresponde al lado más pequeño de nuestro rectángulo áureo, en la secuencia de Fibonacci. Y nos habrá quedado dividido el rectángulo áureo original en un cuadrado y otro rectángulo áureo más pequeño. Repitiendo esta operación podremos dividirlo cuantas veces queramos.
A partir de la sucesión de rectángulos áureos que hemos creado podremos construir la espiral aurea. Si con un arco de circunferencia vamos uniendo sucesivamente los dos vértices opuestos en cada uno de los cuadrados.
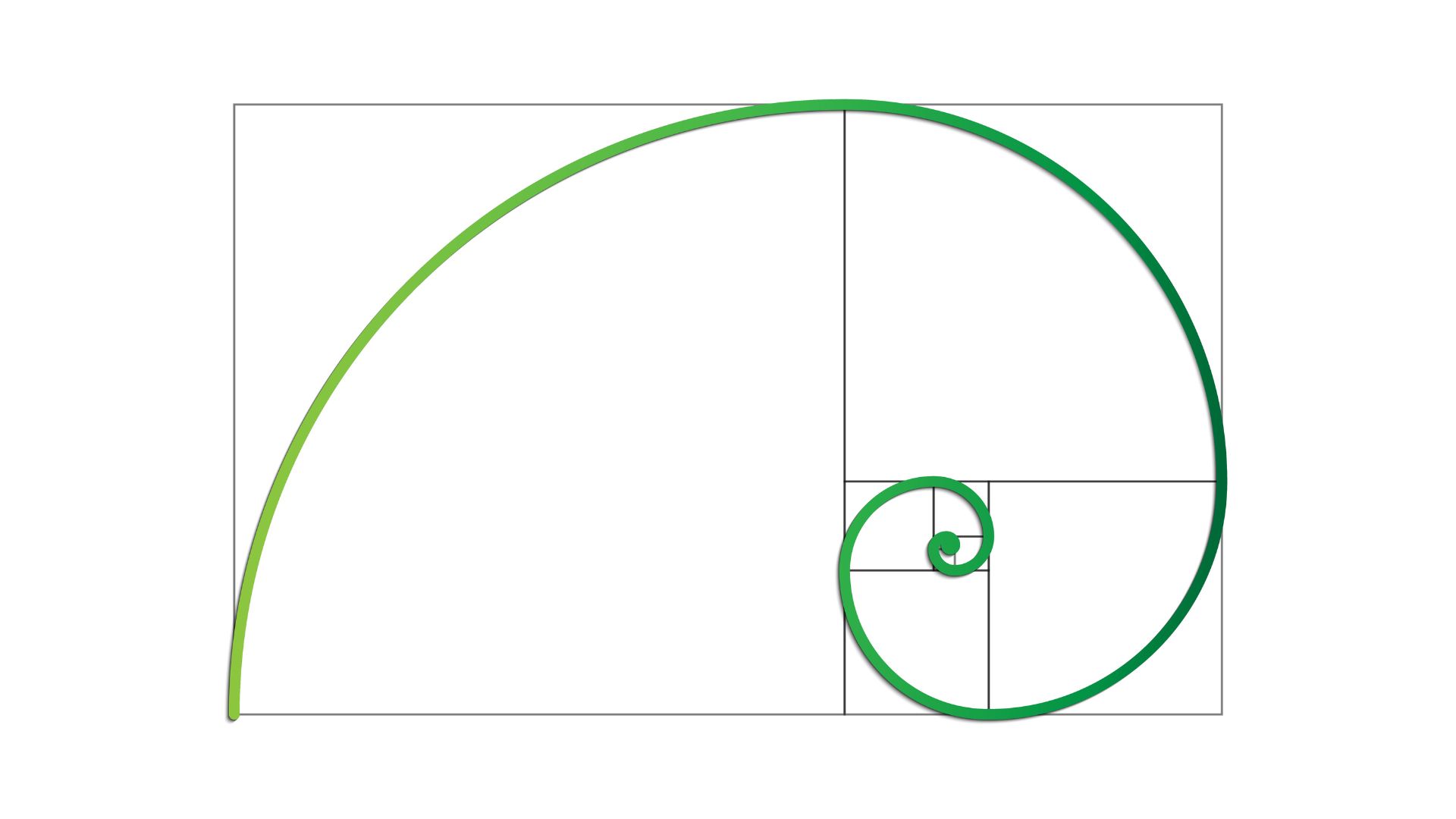
En diseño de interiores podemos valernos del rectángulo áureo para zonificar espacios y de la espiral aurea para crear puntos de interés visual, ambos con un resultado estético muy agradable.
Ejemplos de la proporción aurea en otras construcciones geométricas.
Existen otros muchos ejemplos de construcciones geométricas en las que aparece el número áureo como por magia, por ejemplo:
En un triángulo equilátero cualquiera inscrito en un círculo.
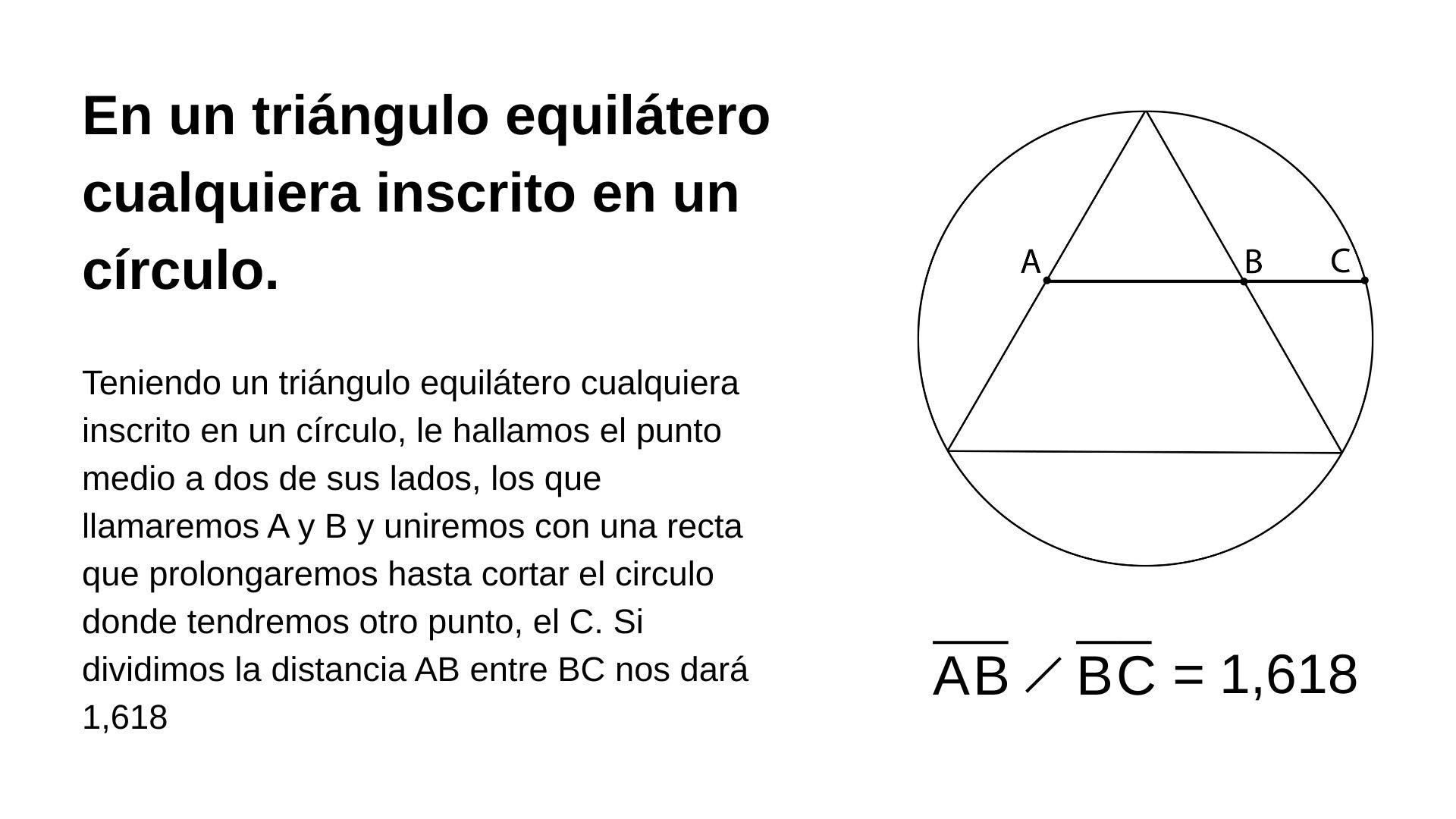
Lo mismo sucede con un cuadrado inscrito en un semicírculo.
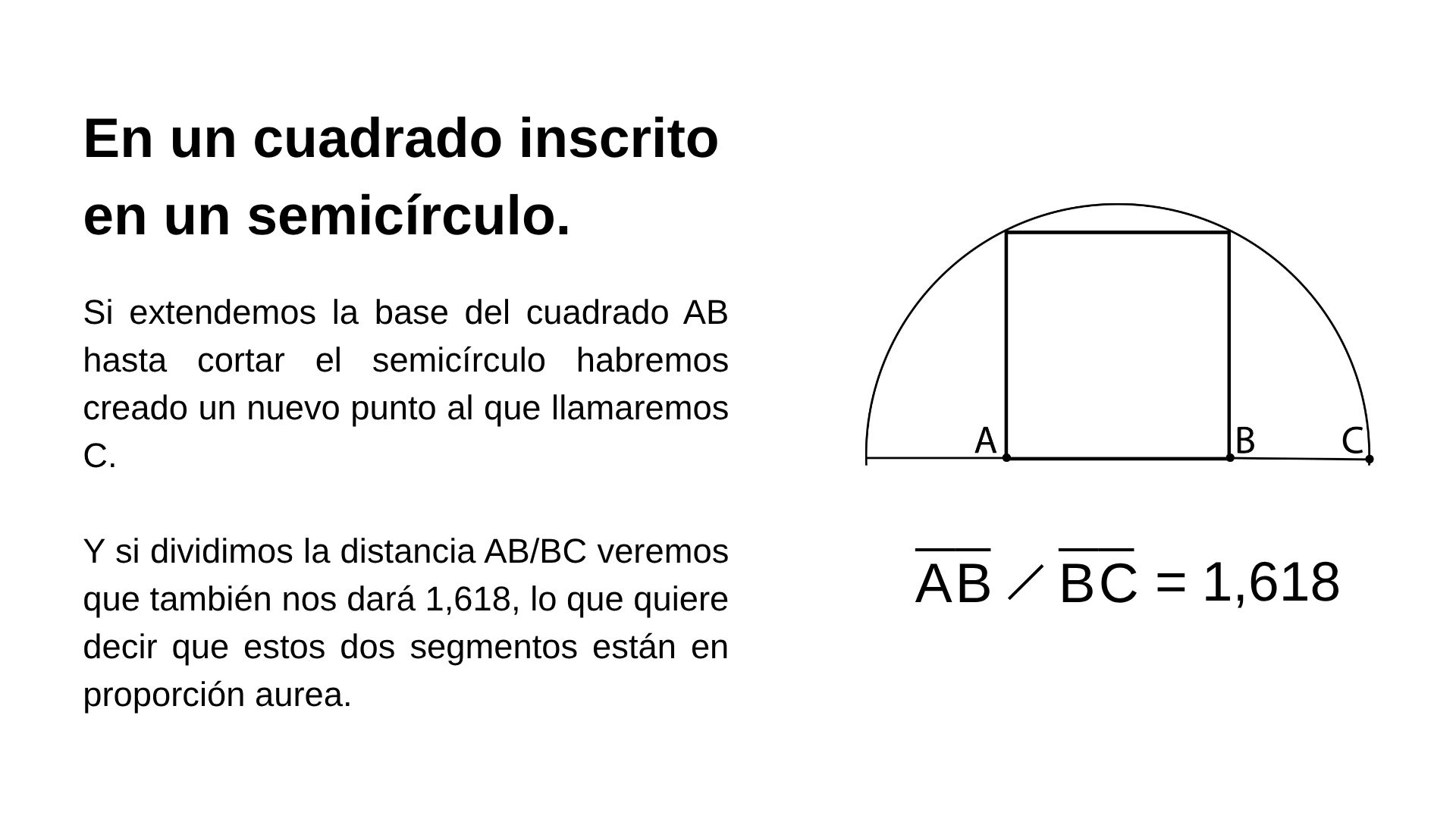
Proporción áurea en los colores.
La proporción áurea ≈1.618 también la podemos utilizar para crear combinaciones de colores armónicas y visualmente agradables. Veamos algunas formas de cómo aplicarla:
Para hallar la Proporción aurea entre valores RGB,
Multiplicamos un valor inicial de un color por 1.618 para obtener otro valor dentro de la misma proporción. Por ejemplo, si comenzamos con R=100: R nos quedará siendo 100, seguidamente calcularemos G multiplicando el 100 de R×1.618 lo que nos dará un resultado aproximadamente igual a162, y B multiplicando el valor que obtuvimos para G es decir 162×1.618 lo que nos dará aproximadamente 261. Pero estos valores han quedado fuera del rango de variación del RGB que va desde 0 hasta 255, por lo que tendremos que ajustarlos.
Existen varias formas para ajustarlo, pero en este caso lo haremos escalándolos, mediante el cálculo de un factor de escala, una forma que nos permitirá ajustar estos valores y que continúen en proporción áurea.
Para el caso del ejemplo que estamos mirando, dividiremos 255 que es el valor máximo del rango de variación del RGB entre 261 que es el valor máximo que en nuestro ejemplo nos ha dado fuera de ese límite. El resultado de esta división será 0,977, así habremos hallado el factor de escala, el que multiplicaremos por cada uno de los valores de RGB que habíamos obtenido.
R = 100 × 0.976 ≈ 98
G = 162 × 0.976 ≈ 158
B = 261 × 0.976 ≈ 255
Y así quedarían nuestros valores ajustados a un rango valido y en proporción aurea:
R = 98
G = 158
B = 255
Para obtener variaciones de tonos: Si tienes un color base, puedes aplicar la proporción áurea a los niveles de brillo o saturación para generar una paleta más armoniosa.
Y Al hacer Distribución en degradados: En los degradados de color, puedes posicionar los puntos clave siguiendo la proporción áurea para obtener transiciones más suaves y equilibradas.
Cómo aplicar la proporción áurea en tus proyectos de diseño.
Es importante recordar que el diseño y la estética no siguen reglas matemáticas exactas. Aunque utilices la proporción áurea en una composición, eso por sí solo no te garantizará que el resultado sea un éxito, hay otros aspectos que también necesitarán de tu atención. Pero la proporción áurea sí puede ser una gran aliada. Te puede ayudar a organizar las ideas, equilibrar los elementos y a lograr diseños armoniosos y visualmente agradables.
Piensa en la proporción áurea como una herramienta de apoyo, no como una regla estricta. Como una guía que te orienta para distribuir mejor los espacios, darle coherencia visual a tu trabajo y que te ayuda a entender mejor los límites de la atención visual y a crear diseños más efectivos.
Conocer cómo funciona la proporción aurea y usarla como punto de partida en tus proyectos, te permitirá lograr composiciones más limpias, equilibradas y visualmente muy agradables.


